A simple method to estimate autocovariance in a semiparametric change-point model

Difference schemes have a long tradition in statistics to estimate, very easily, variance in non-parametric regression. In a series of papers we have shown that this strategy can be used also to estimate auto-covariance even when the regression function exhibits jumps.

Piecewise constant function perturbed by AR(1) error process.

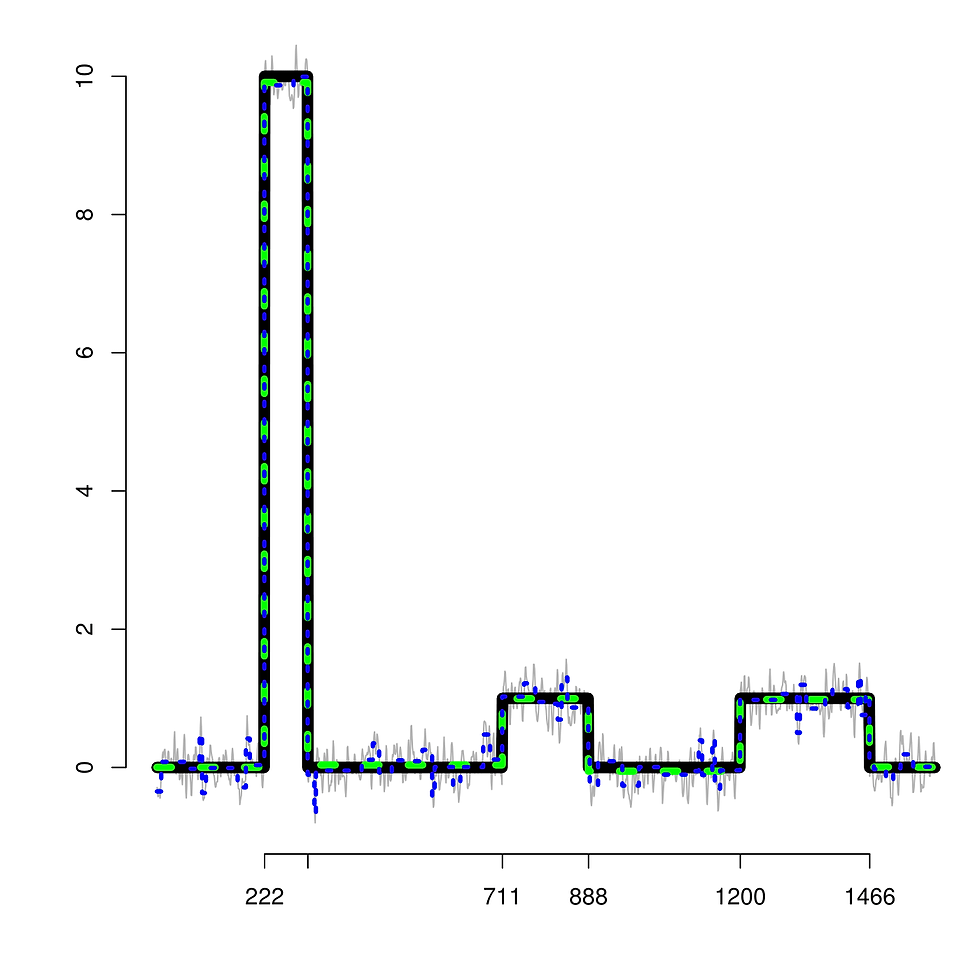
This is the less applied more theoretical part of my research. This story began when I joined Axel Munk's research group in 2013 as a postdoctoral fellow. Part of my project had to do with estimating the correlation structure of some ion channel proteins; there was a real applied problem in all of this after all! In order to estimate that correlation Axel introduced me to the class of difference based estimators.

In my SJS paper, from where I took the plot above, we established that when the total variation of the piecewise constant function is of order o(n) then a class of difference-based estimators of second order and moderate gap is root-n consistent. We also provided an algorithm to estimate a covariance matrix utilizing the autocovariance function obtained from our estimator, we conducted several simulation studies to assess the robustness of our method, and I even introduced a jump segmentation procedure to incorporate the dependence in the error process. You can see the latter in the figure above, it is the green broken line!

Autocovariance function estimation via difference schemes for a semiparametric change point model with m-dependent errors

This is the latest chapter of my wanders with the class of difference-based estimators. In this paper we showed that if you have a data set that looks like the figure above but now the regression function is the sum of a piecewise constant function and a smooth function (think of a sine, cosine or quadratic function), then you can still use difference-based estimators to estimate consistently, at the root-n rate, the correlation function. Obviously for the latter to be totally true the total variation of the piecewise constant component must be of order o(n). The coolest part of our main result is that, asymptotically, the smooth function does not increase the mean squared error of our estimators!

Some software

In dbacf, an R package, I implemented the class of difference-based estimators introduced in my collaboration with Axel Munk. You can download dbacf here. I plan to update the package to incorporate my recent findings, and who knows maybe one day dbacf will make to CRAN!